Distance
Measurement With A Standard Compass
Please feel free to check out our line of Brunton Products These models are made by both Brunton and Silva. You can order any of these models from us.
Please Email Us For Any Information.
Finding Distance With A Compass
An interesting compass application is
to be able to measure the distance across a lake, or large
area with a good degree of accuracy. There is an easy way to
do this with your compass.
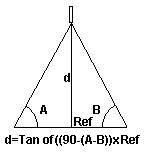
d = (Tan (90 - (A -B))) x Ref
d = Distance (to be calculated)
Tan = Tangent value of the resultant angle
A = Greater value of the two measured bearing angles
B = Lower value of the two measured bearing angles
Ref = Measured reference distance
The method used here is to find a fixed point at the spot you
would like to measure the distance from, to where you are.
You must sight two reference bearings, one on each end of a
measured reference (Ref) distance perpendicular to the spot
to be measured. In practice, the more accurate you measure
this reference distance, and the greater this distance is up
to a 45 degrees total offset, the more exact your results
will be.
Please note that the graphic
shown here is for demonstration only, and is not calibrated
to scale.
- Sight a bearing to the spot that you will measure the distance to, from the exact location where you are standing. This will be bearing or angle (A).
- Walk to a measured perpendicular reference point (Ref) to take another reading to the same spot that will be measured. This will be bearing (B).
- If bearing (B) is greater than bearing (A) then swap the (A) and (B) values. You want to always subtract the smaller number from the greater number.
- Now perform (A) - (B).
- Take this difference and subtract it from 90. Now you have 90-(A-B).
- The next step is to find the Tangent of this final angle or bearing differential. Now you have the Tan of (90-(A-B))
- The last step is to multiply this value by the measured perpendicular reference distance. You now completed the function (Tan(90-(A-B))) x Ref.
- Note that if the first bearing reading is less than 360N (or 0) degrees, and the second bearing reading is past the 360N (or 0) degree value, then you must assume the compass card to exceed the 360N value. For example, if you read 358N degrees for the first value, and 2E degrees for the second value, then the result would be equal to 362 degrees. The differential value would be 4 degrees as required.
For example, if you are looking at a tree across a lake and you want to find its distance from you, sight the first bearing to it. Let us say that it is 210 degrees. Now walk exactly 10 meters perpendicular in relation to the tree (As perpendicular as possible). Next, sight the second bearing to it. Let us say that it is now reading 214 degrees. Now calculate 90 - (214-210). You should get 86. Now find the Tangent of 86. This will give you 14.3 . Multiply this value by the perpendicular reference (Ref) distance (10 meters). This would be (14.3 x 10)=143. The distance (d) to the tree across the lake is 143 meters.
With a very high quality sighting compass, you would be very surprised at the accuracy that can be achieved with this system of measuring distance.
You may download a simple ascii Tangent Table: DEGTAN.TXT You can save this file using your browser. Please use your browser's "Back Key" when finished.
